~今天要分享的是「迴歸分析與邏輯斯迴歸分析實作」~

瞭解了迴歸分析跟邏輯斯迴歸分析的差異後來看看python程式碼要如何撰寫吧！

迴歸分析模型與邏輯斯迴歸分析模型都在sklearn的linear_model套件底下：
#迴歸分析
from sklearn.linear_model import LinearRegression

#邏輯斯迴歸分析
from sklearn.linear_model import LogisticRegression

[程式碼實作]
迴歸分析：使用sklearn的資料集”boston”進行分析

#迴歸分析
import pandas as pd
from sklearn.datasets import load_boston
boston = load_boston()
boston_data=pd.DataFrame(boston['data'],columns=boston['feature_names'])
print("Data：",boston_data.head())
print("=============================")

boston_target=pd.DataFrame(boston['target'],columns=['target'])
print("Target：",boston_target.head())
print("=============================")

X=boston_data[["CRIM",'ZN',"INDUS","CHAS","NOX","RM","AGE","DIS","RAD","TAX","PTRATIO","B","LSTAT"]]
y=boston_target['target'] 
from sklearn.model_selection import train_test_split
X_train, X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)

from sklearn.linear_model import LinearRegression
Linear = LinearRegression()
Linear.fit(X_train,y_train)
Linear.predict(X_test)
print("截距：",Linear.intercept_)
print("相關係數：",Linear.coef_)
print("解釋力：",Linear.score(X_test,y_test))

from sklearn.metrics import mean_squared_error
from math import sqrt
Linear_pred = Linear.predict(X_test)
rmse = sqrt(mean_squared_error(y_test, Linear_pred))
print("rmse: %.3f" % rmse)
print("依變數平均值：",boston_target['target'].mean())

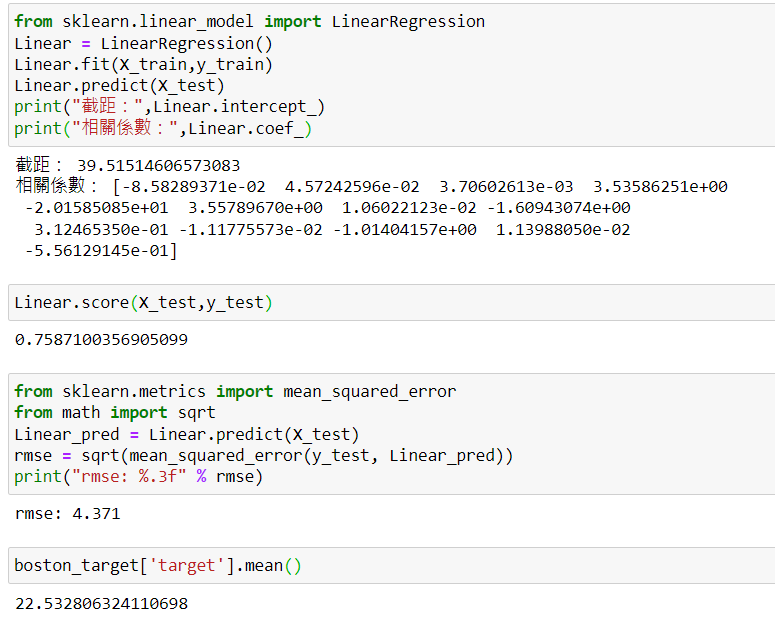
由結果可以得知，迴歸分析的截距約為39.52，而自變數X對目標值依變數Y的相關係數分別是："CRIM"(約-0.086), 'ZN'(約0.046), "INDUS"(約0.004), "CHAS"(約3.536), "NOX"(約-20.159), "RM"(約3.558), "AGE"(約0.011), "DIS"(約-1.609), "RAD"(約0.312), "TAX"(約-0.011), "PTRATIO"(約-1.014), "B"(約0.011), "LSTAT"(約-0.556)。
其中CRIM, NOX, DIS, TAX, PTRATIO, LSTAT對依變數是負相關，其餘都是正相關，而全部自變數裡，” NOX ”對依變數的相關性最大。
另外分析結果也指出，此模型的解釋力約有0.76，且目標變數裡的數據平均值約為22.53，模型誤差只有約4.37，所以是還不錯的模型。

邏輯斯迴歸分析：使用sklearn的資料集”iris”進行分析

#邏輯斯迴歸分析
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
iris_data = pd.DataFrame(iris['data'],columns=iris['feature_names'])
print("Data：",iris_data.head())
print("=============================")

iris_target=pd.DataFrame(iris['target'],columns=['target'])
print("Target：",iris_target.head())
print("=============================")

X=iris_data[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']]
y=iris_target['target'] 
from sklearn.model_selection import train_test_split
X_train, X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)

from sklearn.linear_model import LogisticRegression
Logistic = LogisticRegression()
Logistic.fit(X_train,y_train)

from sklearn.metrics import classification_report,confusion_matrix
Logistic_pred= Logistic.predict(X_test)
print("混淆矩陣：",confusion_matrix(y_test,Logistic_pred))
print("======================================================\n")
print("模型驗證指標：",classification_report(y_test,Logistic_pred))

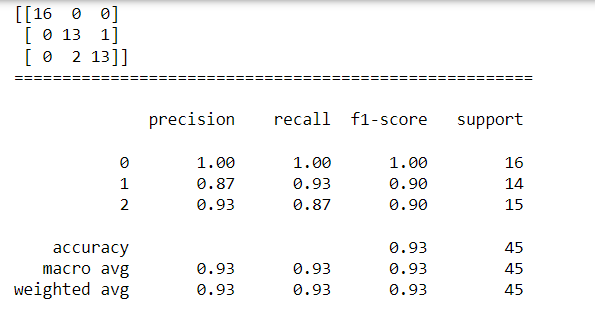
由結果可以得知，測試資料中有一筆原本分類為第2類的樣本被模型預測成第1類，以及兩筆原本分類為第1類的樣本被模型預測成第2類，因此出現了一點誤差，但整體正確率高達0.93，所以是一個很優秀的模型。